Euklid und die Kuppel
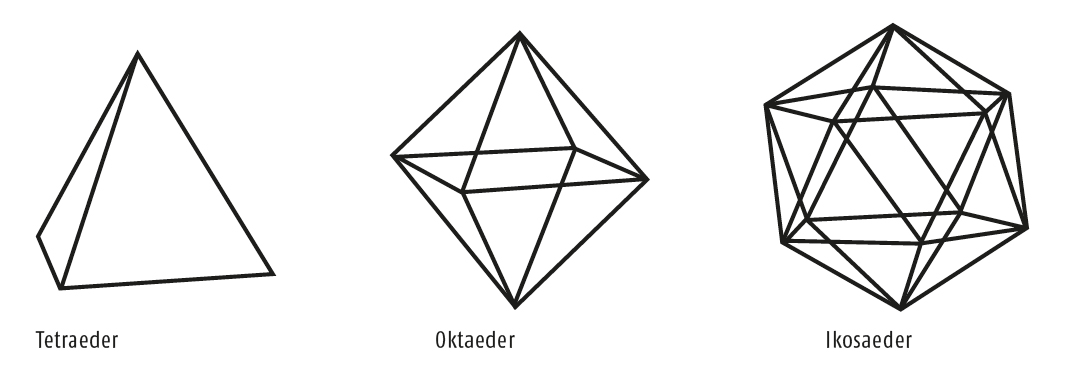
Das Kalthaus des Botanischen Gartens hat die Form einer Halbkugel, die aus vielen Dreiecken aufgebaut ist. Wer aufmerksam davor steht, wird sich nach der Zahl, der Anordnung und der Größe der Dreiecke fragen. Am einfachsten wäre eine Konstruktion aus lauter gleichseitigen Dreiecken, wie bei den folgenden drei Objekten, die zu den „Platonischen Körpern“ gehören:
Das Tetraeder enthält 4, das Oktaeder 8 und das Ikosaeder 20 Dreiecke. Schon Euklid zeigte um 300 v. Chr. in § 18a seines 13. Buches, dass es keine anderen Körper gibt, die von lauter gleichen gleichseitigen Dreiecken begrenzt sind:
Aus 2 Dreiecken oder überhaupt ebenen Flächen lässt sich keine Ecke errichten; aus 3 Dreiecken die der Pyramide [auch Tetraeder genannt], aus 4 die des Oktaeders, aus 5 die des Ikosaeders.
Eine Ecke aus 6 gleichseitigen und gleichwinkeligen Dreiecken, die an einem Punkt zusammengesetzt wären, kann es nicht geben; denn da der Winkel des gleichseitigen Dreiecks 2/3 rechte [das sind 60 Grad] beträgt, würden die 6 zusammen 4 rechte [das sind 360 Grad] ergeben; dies ist unmöglich, denn jede Ecke wird von Winkeln umfasst, die zusammen weniger als 4 rechte ergeben.
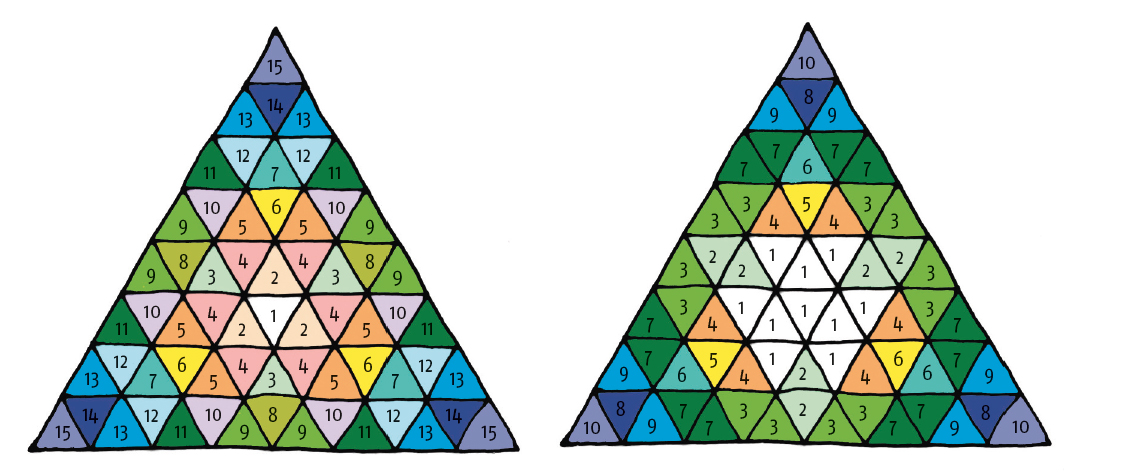
Die Ecken dieser Platonischen Körper liegen auf einer Kugel, der so genannten „Umkugel“. Verbindet man die Ecken entlang der Kugeloberfläche, so erhält man eine Zerlegung der Kugel in gewölbte Dreiecke. Selbst dann, wenn man das Ikosaeder benutzt, werden die entstehenden dreieckigen Fenster bei dem gewünschten Durchmesser der Kuppel von 36 m viel zu groß. Die Idee der Architekten (ausgeführt von H. Emde, Darmstadt) war es nun, zunächst jedes einzelne der 20 Dreiecke des Ikosaeders in 64 = 1 + 3 + … + 13 + 15 gleich große, gleichseitige Teildreiecke zu zerlegen.
Die Eckpunkte dieser Zerlegung des Ikosaeders in kleine Dreiecke werden nach außen auf die Umkugel projiziert und ergeben Näherungen für die späteren Knotenpunkte der Konstruktion. Durch die Projektion auf die Umkugel verändern die vielen kleinen Dreiecke jedoch ihre Proportionen, abhängig von der Lage im großen Dreieck: Sie sind danach nicht mehr gleichseitig und nicht mehr gleich groß. Nach den Argumenten von Euklid ist das ja auch prinzipiell nicht möglich. Eine genaue Zählung ergibt 15 verschiedene Größen von Dreiecken.
Dem Konstrukteur ist durch kleine Verschiebungen der Knotenpunkte eine Korrektur gelungen, nach der insgesamt nur noch 10 verschiedene Größen von Dreiecken und 9 verschieden Längen von Verbindungsrohren benötigt werden.
In den ursprünglichen Ecken des Ikosaeders treffen 5 Rohre aufeinander. Von diesen Knotenpunkten verbleiben 6 auf der oberen Halbkugel: eine im Nordpol und 5 weitere auf gleicher Höhe in der unteren Hälfte. Von allen anderen Knotenpunkten gehen jeweils 6 Rohre aus.
Man kann sich gut vorstellen, wie die Monteure gestöhnt haben, warum nicht alle Verbindungsrohre gleich lang und alle Scheiben gleich groß waren. Aber wer hat schon immer die alten Bücher von Euklid im Kopf?
Autor: Gerd Fischer, TU München
Zahlen
Ikosaeder: 12 Ecken, 30 Kanten, 20 Dreiecke
Anzahl der Fenster: 640 – 10 (für die Ein- und Ausgänge) = 630 Dreiecke
Höhe der Kuppel: 18 m
Grundfläche: ca. 1000 m²
Literatur
Euklid: Die Elemente. Text aus dem Griechischen übersetzt von Clemens Thaer; Wissenschaftliche Buchgesellschaft Darmstadt 1980.
Hilbert, D. & S. Cohn-Vossen: Anschauliche Geometrie. Verlag von Julius Springer, Berlin 1932.